|| The Globe ||
Mercator ||
Transverse Mercator || Oblique
Mercator || Space Oblique Mercator ||
Miller Cylindrical ||
Robinson || Sinusoidal Equal Area
|| Orthographic ||
Stereographic ||
|| Gnomonic ||
Azimuthal Equidistant ||
Lambert Azimuthal Equal Area ||
Albers Equal Area Conic ||
Lambert Conformal Conic ||
Equidistant Conic (Simple Conic)
|| Polyconic ||
|| Bipolar Oblique Conic Conformal ||
Summary Table ||
General Notes ||
Map Projections
|
Gerardus Mercator
(1512-1594). Frontispiece to Mercator's Atlas sive
Cosmographicae, 1585-1595. Courtesy of the Library
of Congress, Rare Book Division, Lessing J. Rosenwald
Collection. |
A map projection is used to
portray all or part of the round Earth on a flat surface. This
cannot be done without some distortion.
Every projection has its own
set of advantages and disadvantages. There is no "best"
projection.
The mapmaker must select the
one best suited to the needs, reducing distortion of the most
important features.
Mapmakers and mathematicians
have devised almost limitless ways to project the image of the
globe onto paper. Scientists at the U. S. Geological Survey have
designed projections for their specific needs—such as the Space
Oblique Mercator, which allows mapping from satellites with
little or no distortion.
This document gives the key
properties, characteristics, and preferred uses of many
historically important projections and of those frequently used
by mapmakers today.
Which ones best suit your
needs?
Every flat map misrepresents the surface of the Earth in some
way. No map can rival a globe in truly representing the surface
of the entire Earth. However, a map or parts of a map can show
one or more—but never all—of the following: True directions.
True distances. True areas. True shapes.
For example, the basic Mercator projection is unique; it
yields the only map on which a straight line drawn anywhere
within its bounds shows a particular type of direction, but
distances and areas are grossly distorted near the map's polar
regions.
On an equidistant map, distances are true only along
particular lines such as those radiating from a single point
selected as the center of the projection. Shapes are more or
less distorted on every equal-area map. Sizes of areas are
distorted on conformal maps even though shapes of small areas
are shown correctly. The degree and kinds of distortion vary
with the projection used in making a map of a particular area.
Some projections are suited for mapping large areas that are
mainly north-south in extent, others for large areas that are
mainly east-west in extent, and still others for large areas
that are oblique to the Equator.
The scale of a map on any projection is always important and
often crucial to the map's usefulness for a given purpose. For
example, the almost grotesque distortion that is obvious at high
latitudes on a small-scale Mercator map of the world disappears
almost completely on a properly oriented large-scale Transverse
Mercator map of a small area in the same high latitudes. A
large-scale (1:24,000) 7.5-minute USGS Topographic Map based on
the Transverse Mercator projection is nearly correct in every
respect.
A basic knowledge of the properties of commonly used
projections helps in selecting a map that comes closest to
fulfilling a specific need.
|| Top || Main table
of contents ||
The Globe
 Directions—True
Distances—True
Shapes—True
Areas—TrueGreat circles—The
shortest distance between any two points on the surface
of the Earth can be found quickly and easily along a
great circle.
Disadvantages:
- Even the largest globe has a very small scale
and shows relatively little detail.
- Costly to reproduce and update.
- Difficult to carry around.
- Bulky to store.
On the globe:
Parallels are parallel and spaced equally on meridians.
Meridians and other arcs of great circles are straight
lines (if looked at perpendicularly to the Earth's
surface). Meridians converge toward the poles and
diverge toward the Equator.
Meridians are equally spaced on the parallels, but
their distances apart decreases from the Equator to the
poles. At the Equator, meridians are spaced the same as
parllels. Meridians at 60° are half as far apart as
parallels. Parallels and meridians cross at right
angles. The area of the surface bounded by any two
parallels and any two meridians (a given distance apart)
is the same anywhere between the same two parallels.
The scale factor at each point is the same in any
direction. |
After Robinson and Sale, Elements of
Cartography (3rd edition, John Wiley & Sons, Inc. 1969,
p.212).
|| Top || Main table
of contents ||
Mercator
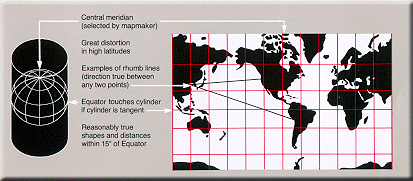 Used
for navigation or maps of equatorial regions. Any
straight line on the map is a rhumb line
(line of constant direction). Directions
along a rhumb line are true between any two
points on map, but a rhumb line is usually not
the shortest distance between points. (Sometimes used
with Gnomonic map on which any straight line is on a
great circle and shows shortest path between two
points).Distances are true only
along Equator, but are reasonably correct within 15° of
Equator; special scales can be used to measure distances
along other parallels. Two particular parallels can be
made correct in scale instead of the Equator.
Areas and shapes of large areas are
distorted. Distortion increases away
from Equator and is extreme in polar regions. Map,
however, is conformal in that angles
and shapes within any small area (such as that shown by
USGS topographic map) is essentially true.
The map is not perspective, equal
area, or equidistant.
Equator and other parallels are straight lines
(spacing increases toward poles) and meet meridians
(equally spaced straight lines) at right angles. Poles
are not shown.
Presented by Mercator in 1569.
Cylindrical— Mathematically
projected on a cylinder tangent to the Equator.
(Cylinder may also be secant.) |
|| Top || Main table
of contents ||
Transverse Mercator
 Used
by USGS for many quadrangle maps at scales from 1:24,000
to 1:250,000; such maps can be joined at their edges
only if they are in the same zone with one central
meridian. Also used for mapping large areas that are
mainly north-south in extent.Distances
are true only along the central meridian
selected by the mapmaker or else along two lines
parallel to it, but all distances, directions, shapes,
and areas are reasonably accurate within 15° of the
central meridian. Distortion of
distances, directions, and size of areas increases
rapidly outside the 15° band. Because the map is
conformal, however, shapes and angles within
any small area (such as that shown by a USGS topographic
map) are essentially true.
Graticule spacing increases away
from central meridian. Equator is straight. Other
parallels are complex curves concave toward nearest
pole.
Central meridian and each meridian 90° from it are
straight. Other meridians are complex curves concave
toward central meridian.
Presented by Lambert in 1772.
Cylindrical—Mathematically projected
on cylinder tangent to a meridian. (Cylinder may also be
secant.) |
|| Top || Main table
of contents ||
Oblique Mercator
 Used
to show regions along a great circle
other than the Equator or a meridian, that is, having
their general extent oblique to the Equator. This kind
of map can be made to show as a straight line the
shortest distance between any two preselected points
along the selected great circle.Distances
are true only along the great circle (the line
of tangency for this projection), or along two lines
parallel to it. Distances, directions, areas, and shapes
are fairly accurate within 15° of the great circle.
Distortion of areas, distances, and
shapes increases away from the great circle. It is
excessive toward the edges of a world map except near
the path of the great circle.
The map is conformal, but
not perspective, equal area, or equidistant.
Rhumb lines are curved.
Graticule spacing increases away
from the great circle but conformality is retained. Both
poles can be shown. Equator and other parallels are
complex curves concave toward nearest pole. Two
meridians 180° apart are straight lines; all others are
complex curves concave toward the great circle.
Developed 1900-50 by Rosenmund, Laborde, Hotine et
al.
Cylindrical—Mathematically projected
on a cylinder tangent, (or secant) along any great
circle but the Equator or a meridian.
Directions, distances, and areas reasonably accurate
only within 15° of the line of tangency. |
|| Top || Main table
of contents ||
Space Oblique Mercator
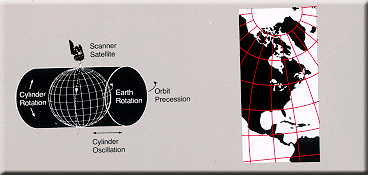 This
new space-age conformal projection was developed by the
USGS for use in Landsat images because
there is no distortion along the curved groundtrack
under the satellite. Such a projection is needed for the
continuous mapping of satellite images, but it is useful
only for a relatively narrow band along the groundtrack.
Space Oblique Mercator maps show a satellite's
groundtrack as a curved line that is continuously true
to scale as orbiting continues.
Extent of the map is defined by orbit of the
satellite.
Map is basically conformal,
especially in region of satellite scanning.
Developed in 1973-79 by A. P. Colvocoresses, J. P.
Snyder, and J. L. Junkins. |
|| Top || Main table
of contents ||
Miller Cylindrical
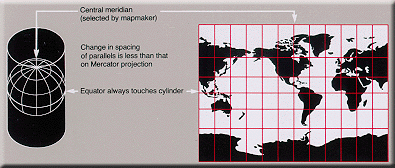 Used
to represent the entire Earth in a rectangular frame.
Popular for world maps. Looks like Mercator but is not
useful for navigation. Shows poles as straight lines.
Avoids some of the scale exaggerations
of the Mercator but shows neither shapes nor areas
without distortion.
Directions are true only along the
Equator. Distances are true only along
the Equator. Distortion of distances,
areas, and shapes is extreme in high latitudes.
Map is not equal area, equidistant,
conformal or perspective.
Presented by O. M. Miller in 1942.
Cylindrical—Mathematically projected
onto a cylinder tangent at the Equator. |
|| Top || Main table
of contents ||
Robinson
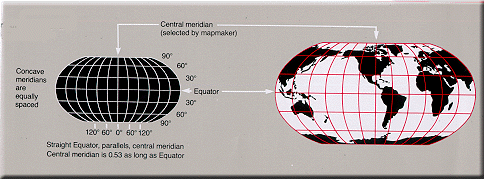 Uses
tabular coordinates rather than mathematical formulas to
make the world "look right." Better balance of
size and shape of high-latitude lands than in
Mercator, Van der Grinten, or Mollweide. Soviet Union,
Canada, and Greenland truer to size, but Greenland
compressed.Directions true along all
parallels and along central meridian. Distances
constant along Equator and other parallels, but scales
vary. Scale true along 38° N & S,
constant along any given parallel, same along N & S
parallels same distance from. Equator.
Distortion: All points have some. Very low
along Equator and within 45° of center. Greatest near
the poles.
Not conformal, equal area,
equidistant, or perspective.
Used in Goode's Atlas,
adopted for
National Geographic's world maps in 1988,
appears in growing number of other publications, may
replace Mercator in many classrooms.
Presented by Arthur H. Robinson in 1963.
Pseudocylindrical or orthophanic
("right appearing") projection. |
|| Top || Main table
of contents ||
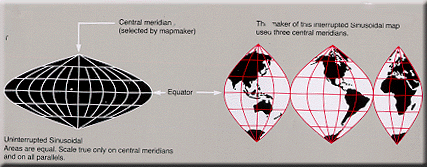
Sinusoidal Equal Area
 Used
frequently in atlases to show distribution patterns.
Used by the USGS to show prospective hydrocarbon
provinces and sedimentary basins of the world. Has been
used for maps of Africa, South America, and other large
areas that are mainly north-south in extent.An easily
plotted equal-area projection for world maps. May have a
single central meridian or, in interrupted form, several
central meridians.
Graticule spacing retains property
of equivalence of area. Areas on map
are proportional to same areas on the Earth.
Distances are correct along all parallels and
the central meridian(s). Shapes are
increasingly distorted away from the central meridian(s)
and near the poles.
Map is not conformal, perspective,
or equidistant.
Used by Cossin and Hondius, beginning in 1570. Also
called the Sanson-Flamsteed.
Pseudocylindrical—Mathematically
based on a cylinder tangent to the Equator. |
|| Top || Main table
of contents ||
Orthographic
 Used
for perspective views of the Earth, Moon, and other
planets. The Earth appears as it would on a photograph
from deep space.
Directions are true only
from center point of projection. Scale
decreases along all lines radiating from center point of
projection. Any straight line through center point is a
great circle. Areas and shapes are
distorted by perspective; distortion increases away from
center point.
Map is perspective but not
conformal or equal area. In the polar aspect, distances
are true along the Equator and all other parallels.
The Orthographic projection was known to Egyptians
and Greeks 2,000 years ago.
Azimuthal—Geometrically projected
onto a plane. Point of projection is at infinity. |
|| Top || Main table
of contents ||
Stereographic
 Used
by the USGS for maps of Antarctica and American
Geographical Society for Arctic and Antarctic maps. May
be used to map large continent-sized areas of similar
extent in all directions. Used in geophysics to solve
spherical geometry problems. Polar aspects used for
topographic maps and charts for navigating in latitudes
above 80°.Directions true only
from center point of projection. Scale
increases away from center point. Any straight line
through center point is a great circle.
Distortion of areas and large shapes
increases away from center point.
Map is conformal and perspective but
not equal area or equidistant.
Dates from 2nd century B.C. Ascribed to Hipparchus.
Azimuthal—Geometrically projected on
a plane. Point of projection is at surface of globe
opposite the point of tangency. |
|| Top || Main table
of contents ||
Gnomonic
 Used
along with the Mercator by some navigators to find the
shortest path between two points. Used in seismic work
because seismic waves tend to travel along great
circles.Any straight line drawn on the map is on a
great circle, but directions
are true only from center point of projection.
Scale increases very rapidly away from
center point. Distortion of shapes and
areas increases away from center point.
Map is perspective (from the center of the Earth onto
a tangent plane) but not conformal,
equal area, or equidistant.
Considered to be the oldest projection. Ascribed to
Thales, the father of abstract geometry, who lived in
the 6th century B.C.
Azimuthal—Geometrically projected on
a plane. Point of projection is the center of a globe. |
|| Top || Main table
of contents ||
Azimuthal Equidistant
 Used
for large-scale mapping of Micronesia. Useful for
showing airline distances from center point of
projection. Useful for seismic and radio work. Oblique
aspect used for atlas maps of continents and world maps
for radio and aviation use. Polar aspect used for world
maps, maps of polar hemispheres, and United Nations
emblem.Distances and
directions to all places true only
from center point of projection. Distances correct
between points along straight lines through center. All
other distances incorrect . Any straight line drawn
through center point is on a great circle.
Distortion of areas and shapes
increases away from center point.
Azimuthal—Mathematically projected
on a plane tangent to any point on globe. Polar aspect
is tangent only at pole. |
|| Top || Main table
of contents ||
Lambert Azimuthal Equal Area
 Used
by the USGS in its National Atlas and Circum-Pacific Map
Series. Suited for regions extending equally in all
directions from center points, such as Asia and Pacific
Ocean.Areas on the map are shown in
true proportion to the same areas on the Earth.
Quadrangles (bounded by two meridians and two parallels)
at the same latitude are uniform in area.
Directions are true only
from center point. Scale decreases
gradually away from center point. Distortion
of shapes increases away from center point. Any straight
line drawn through center point is on a great
circle.
Map is equal area but not conformal,
perspective, or equidistant.
Presented by Lambert in 1772.
Azimuthal—Mathematically projected
on a plane tangent to any point on globe. Polar aspect
is tangent only at pole. |
|| Top || Main table
of contents ||
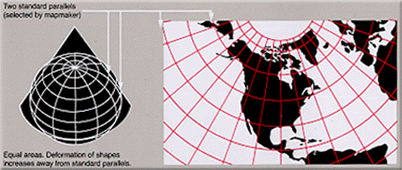
Albers Equal Area Conic
 Used
by USGS for maps showing the conterminous United States
(48 states) or large areas of the United States. Well
suited for large countries or other areas that are
mainly east-west in extent and that require equal-area
representation. Used for many thematic maps.Maps
showing adjacent areas can be joined at their edges only
if they have the same standard parallels (parallels of
no distortion) and the same scale.
All areas on the map are
proportional to the same areas on the Earth.
Directions are reasonably accurate in limited
regions. Distances are true on both
standard parallels. Maximum scale error is 1 ¼% on map
of conterminous States with standard parallels of 29 ½°N
and 45 ½°N. Scale true only along
standard parallels.
USGS maps of the conterminous 48 States, if based on
this projection have standard parallels 29 ½°N and 45
½°N. Such maps of Alaska use standard parallels 55°N and
65°N, and maps of Hawaii use standard parallels 8°N and
18°N.
Map is not conformal, perspective,
or equidistant.
Presented by H. C. Albers in 1805.
Conic—Mathematically projected on a
cone conceptually secant at two standard parallels. |
|| Top || Main table
of contents ||
Lambert Conformal Conic
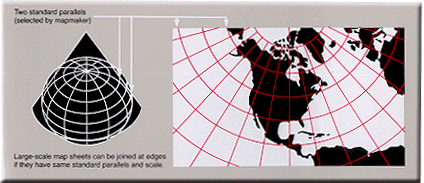 Used
by USGS for many 7.5- and 15-minute topographic maps and
for the State Base Map series. Also used to show a
country or region that is mainly east-west in extent.
One of the most widely used map projections in the
United States today. Looks like the Albers Equal Area
Conic, but graticule spacings differ.
Retains conformality. Distances true
only along standard parallels; reasonably
accurate elsewhere in limited regions.
Directions reasonably accurate.
Distortion of shapes and areas minimal at, but
increases away from standard parallels. Shapes
on large-scale maps of small areas essentially true.
Map is conformal but not
perspective, equal area, or equidistant.
For USGS Base Map series for the 48 conterminous
States, standard parallels are 33°N and 45°N (maximum
scale error for map of 48 States is 2 ½%). For USGS
Topographic Map series (7.5- and 15-minute), standard
parallels vary. For aeronautical charts of Alaska, they
are 55°N and 65°N; for the National Atlas of Canada,
they are 49°N and 77°N.
Presented by Lambert in 1772.
Conic—Mathematically projected on a
cone conceptually secant at two standard parallels. |
|| Top || Main table
of contents ||
Equidistant Conic (Simple
Conic)
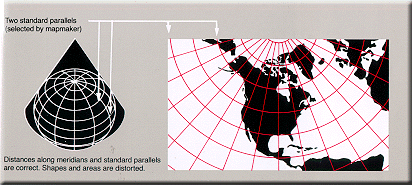 Used
in atlases to show areas in the middle latitudes. Good
for showing regions within a few degrees of latitude and
lying on one side of the Equator. (One example, the
Kavraisky No. 4, is an Equidistant Conic projection in
which standard parallels are chosen to minimize overall
error.)Distances are true only
along all meridians and along one or two standard
parallels. Directions, shapes and areas
are reasonably accurate, but distortion
increases away from standard parallels.
Map is not conformal, perspective,
or equal area, but a compromise between Lambert
Conformal Conic and Albers Equal Area Conic.
Prototype by Ptolemy, 150 A.D. Improved by De I'Isle
about 1745.
Conic—Mathematically projected on a
cone tangent at one parallel or conceptually secant at
two parallels. |
|| Top || Main table
of contents ||
Polyconic
 Used
almost exclusively for large-scale mapping in the United
States until the 1950's. Now nearly obsolete, and no
longer used by USGS for new plotting in its Topographic
Map series. Best suited for areas with a north-south
orientation.Directions are true
only along central meridian. Distances
are true only along each parallel and along
central meridian. Shapes and areas true
only along central meridian. Distortion
increases away from central meridian.
Map is a compromise of many properties. It is
not conformal, perspective, or equal area.
Apparently originated about 1820 by Hassler.
Conic—Mathematically based on an
infinite number of cones tangent to an infinite number
of parallels. |
|| Top || Main table
of contents ||
Bipolar Oblique Conic Conformal
 This
"tailor-made" projection is used to
show one or both of the American continents. Outlines in
the projection diagram represent areas shown on USGS
Basement and Tectonic Maps of North America.
Scale is true along two lines ("transformed
standard parallels") that do not lie along any meridian
or parallel. Scale is compressed between these lines and
expanded beyond them. Scale is generally good but error
is as much as 10% at the edge of the projection as used.
Graticule spacing increases away
from the lines of true scale but retains the property of
conformality except for a small deviation from
conformality where the two conic projections join.
Map is conformal but not equal area,
equidistant, or perspective.
Presented by O. M. Miller and W. A. Briesemeister in
1941.
Conic—Mathematically based on two
cones whose apexes are 104° apart and which conceptually
are obliquely secant to the globe along lines following
the trend of North and South America. |
|| Top || Main table
of contents ||
Summary Tables
Summary of Projection Properties
|
| Key:* = Yes x= Partly |
|
Projection |
Type |
Conformal |
Equal area |
Equidistant |
True
direction |
Perspective |
Compromise |
Straight
rhumbs |
|
Globe |
Sphere |
* |
* |
* |
* |
|
|
|
|
Mercator |
Cylindrical |
* |
|
|
x |
|
|
* |
|
Transverse Mercator |
Cylindrical |
* |
|
|
|
|
|
|
|
Oblique Mercator |
Cylindrical |
* |
|
|
|
|
|
|
|
Space Oblique Mercator |
Cylindrical |
* |
|
|
|
|
|
|
|
Miller Cylindrical |
Cylindrical |
|
|
|
|
|
* |
|
|
Robinson |
Pseudo-
cylindrical |
|
|
|
|
|
* |
|
Sinusoidal Equal
Area |
Pseudo-
cylindrical |
|
* |
x |
|
|
|
|
|
Orthographic |
Azimuthal |
|
|
|
x |
* |
|
|
|
Stereographic |
Azimuthal |
* |
|
|
x |
* |
|
|
|
Gnomonic |
Azimuthal |
|
|
|
x |
* |
|
|
|
Azimuthal Equalidistant |
Azimuthal |
|
|
x |
x |
|
|
|
|
Lambert Azimuthal Equal Area |
Azimuthal |
|
* |
|
x |
|
|
|
|
Albers Equal Area Conic |
Conic |
|
* |
|
|
|
|
|
|
Lambert Conformal Conic |
Conic |
* |
|
|
x |
|
|
|
|
Equidistant Conic |
Conic |
|
|
x |
|
|
|
|
|
Polyonic |
Conic |
|
|
x |
|
|
* |
|
|
Biplolar Oblique Conic Conformal |
Conic |
* |
|
|
|
|
|
|
Summary of Areas Suitable of Mapping with
Projections
|
| Key:* = Yes x = Partly |
|
Projection |
Type |
World |
Hemisphere |
Continent/
Ocean |
Region/
sea |
Medium
scale |
Large scale |
|
Globe |
Sphere |
* |
|
|
|
|
|
|
Mercator |
Cylindrical |
x |
|
|
* |
|
|
|
Transverse Mercator |
Cylindrical |
|
|
* |
* |
* |
* |
|
Oblique Mercator |
Cylindrical |
|
|
* |
* |
* |
* |
|
Space Oblique Mercator |
Cylindrical |
|
|
|
|
|
* |
|
Miller Cylindrical |
Cylindrical |
* |
|
|
|
|
|
|
Robinson |
Pseudo-
cylindrical |
* |
|
|
|
|
|
Sinusoidal Equal
Area |
Pseudo-
cylindrical |
* |
|
* |
|
|
|
|
Orthographic |
Azimuthal |
|
x |
|
|
|
|
|
Stereographic |
Azimuthal |
|
* |
* |
* |
* |
* |
|
Gnomonic |
Azimuthal |
|
|
|
x |
|
|
|
Azimuthal Equalidistant |
Azimuthal |
x |
* |
* |
* |
|
x |
|
Lambert Azimuthal Equal Area |
Azimuthal |
|
* |
* |
* |
|
|
|
Albers Equal Area Conic
|
Conic |
|
|
* |
* |
* |
|
|
Lambert Conformal Conic |
Conic |
|
|
* |
* |
* |
* |
|
Equidistant Conic |
Conic |
|
|
* |
* |
|
|
|
Polyonic |
Conic |
|
|
|
|
x |
x |
|
Biplolar Oblique ConicConformal |
Conic |
|
|
* |
|
|
|
Summary of Projection General Use
|
| Key:* = Yes |
|
Projection |
Type |
Topographic
Maps |
Geological
Maps |
Thematic
Maps |
Presentations |
Navigation |
USGS
Maps |
|
Globe |
Sphere |
|
|
* |
* |
|
|
|
Mercator |
Cylindrical |
* |
* |
|
|
* |
* |
|
Transverse Mercator |
Cylindrical |
* |
* |
|
|
|
* |
|
Oblique Mercator |
Cylindrical |
* |
|
|
|
|
* |
|
Space Oblique Mercator |
Cylindrical |
* |
|
|
|
|
* |
|
Miller Cylindrical |
Cylindrical |
|
|
* |
|
|
* |
|
Robinson |
Pseudo-
cylindrical |
|
|
* |
* |
|
|
Sinusoidal Equal
Area |
Pseudo-
cylindrical |
|
|
* |
|
|
* |
|
Orthographic |
Azimuthal |
|
|
|
|
|
* |
|
Stereographic |
Azimuthal |
* |
* |
|
|
* |
* |
|
Gnomonic |
Azimuthal |
|
|
|
* |
* |
|
|
Azimuthal Equalidistant |
Azimuthal |
* |
|
|
|
|
* |
|
Lambert Azimuthal Equal Area |
Azimuthal |
|
|
* |
* |
|
* |
|
Albers Equal Area Conic |
Conic |
|
|
* |
* |
|
* |
|
Lambert Conformal Conic |
Conic |
* |
* |
|
* |
* |
* |
|
Equidistant Conic |
Conic |
|
|
|
|
|
|
|
Polyonic |
Conic |
* |
|
|
|
|
* |
|
Biplolar Oblique Conic Conformal |
Conic |
|
* |
|
|
|
* |
|| Top || Main table
of contents ||
General Notes
Azimuth—The angle measured in degrees
between a base line radiating from a center point and another
line radiating from the same point. Normally, the base line
points North, and degrees are measured clockwise from the base
line.
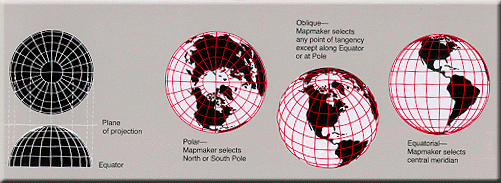
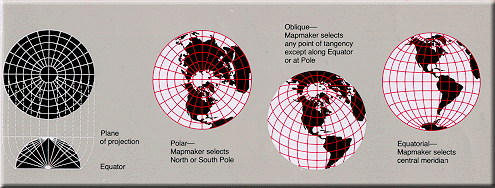
Aspect—Individual azimuthal map projections
are divided into three aspects: the polar aspect which is
tangent at the pole, the equatorial aspect which is tangent at
the Equator, and the oblique aspect which is tangent anywhere
else. (The word "aspect" has replaced the word "case" in the
modern cartographic literature.)
Conformality—A map projection is conformal
when at any point the scale is the same in every direction.
Therefore, meridians and parallels intersect at right angles and
the shapes of very small areas and angles with very short sides
are preserved. The size of most areas, however, is distorted.
Developable surface—A developable surface is
a simple geometric form capable of being flattened without
stretching. Many map projections can then be grouped by a
particular developable surface: cylinder, cone, or plane.
Equal areas—A map projection is equal area
if every part, as well as the whole, has the same area as the
corresponding part on the Earth, at the same reduced scale. No
flat map can be both equal area and conformal.
Equidistant—Equidistant maps show true
distances only from the center of the projection or along a
special set of lines. For example, an Azimuthal Equidistant map
centered at Washington shows the correct distance between
Washington and any other point on the projection. It shows the
correct distance between Washington and San Diego and between
Washington and Seattle. But it does not show the correct
distance between San Diego and Seattle. No flat map can be both
equidistant and equal area.
Graticule—The graticule is the spherical
coordinate system based on lines of latitude and longitude.
Great circle—A circle formed on the surface
of a sphere by a plane that passes through the center of the
sphere. The Equator, each meridian, and each other full
circumference of the Earth forms a great circle. The arc of a
great circle shows the shortest distance between points on the
surface of the Earth.
Linear scale—Linear scale is the relation
between a distance on a map and the corresponding distance on
the Earth. Scale varies from place to place on every map. The
degree of variation depends on the projection used in making the
map.
Map projection—A map projection is a
systematic representation of a round body such as the Earth or a
flat (plane) surface. Each map projection has specific
properties that make it useful for specific purposes.
Rhumb line—A rhumb line is a line on the
surface of the Earth cutting all meridians at the same angle. A
rhumb line shows true direction. Parallels and meridians, which
also maintain constant true directions, may be considered
special cases of the rhumb line. A rhumb line is a straight line
on a Mercator projection. A straight rhumb line does not show
the shorter distance between points unless the points are on the
Equator or on the same meridian.
|| Top || Main table
of contents ||
How To Obtain More Information
For information on these and other products and services,
contact one of customer service representatives at
800-248-6277 or
Sales@GeoMart.com
|| Top || Main
table of contents ||
|
